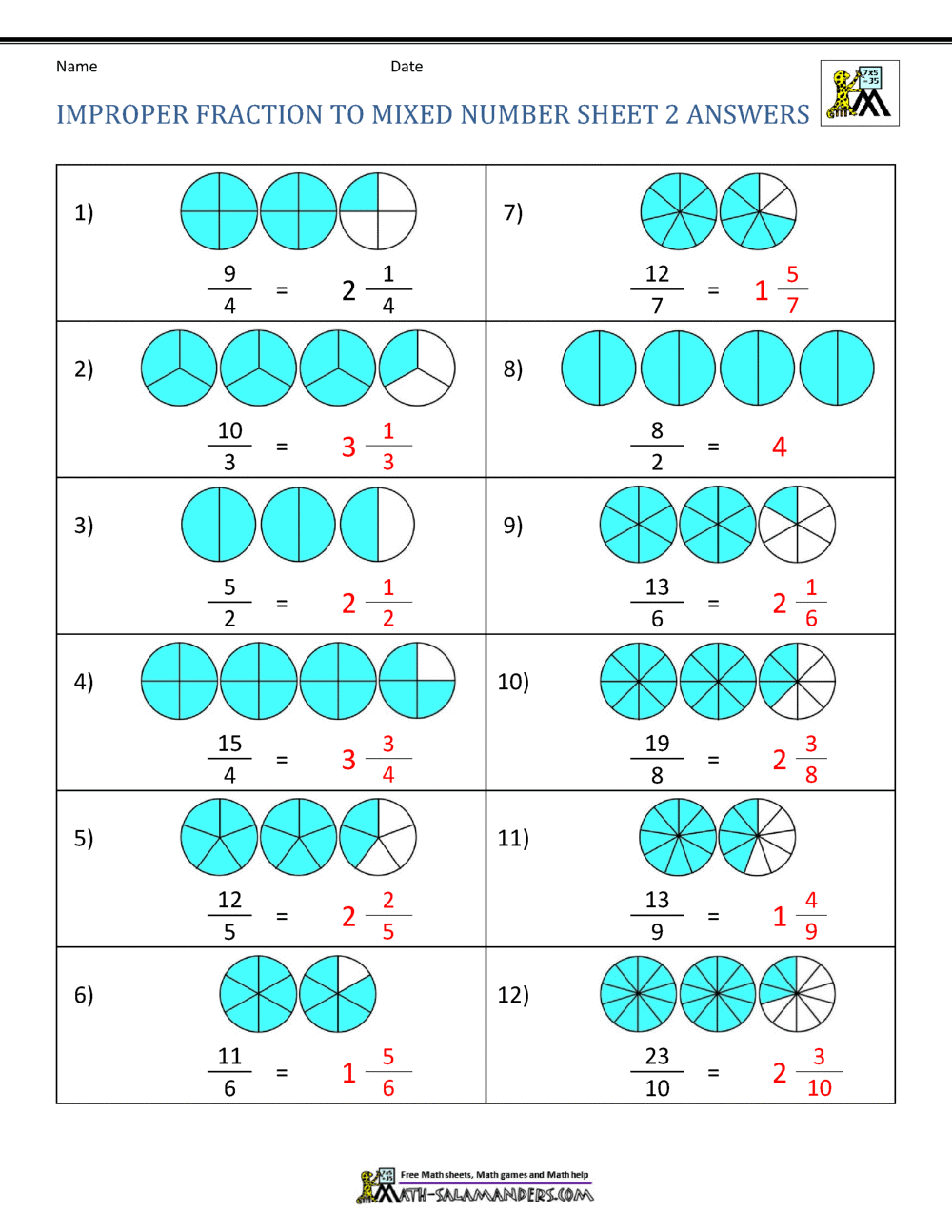
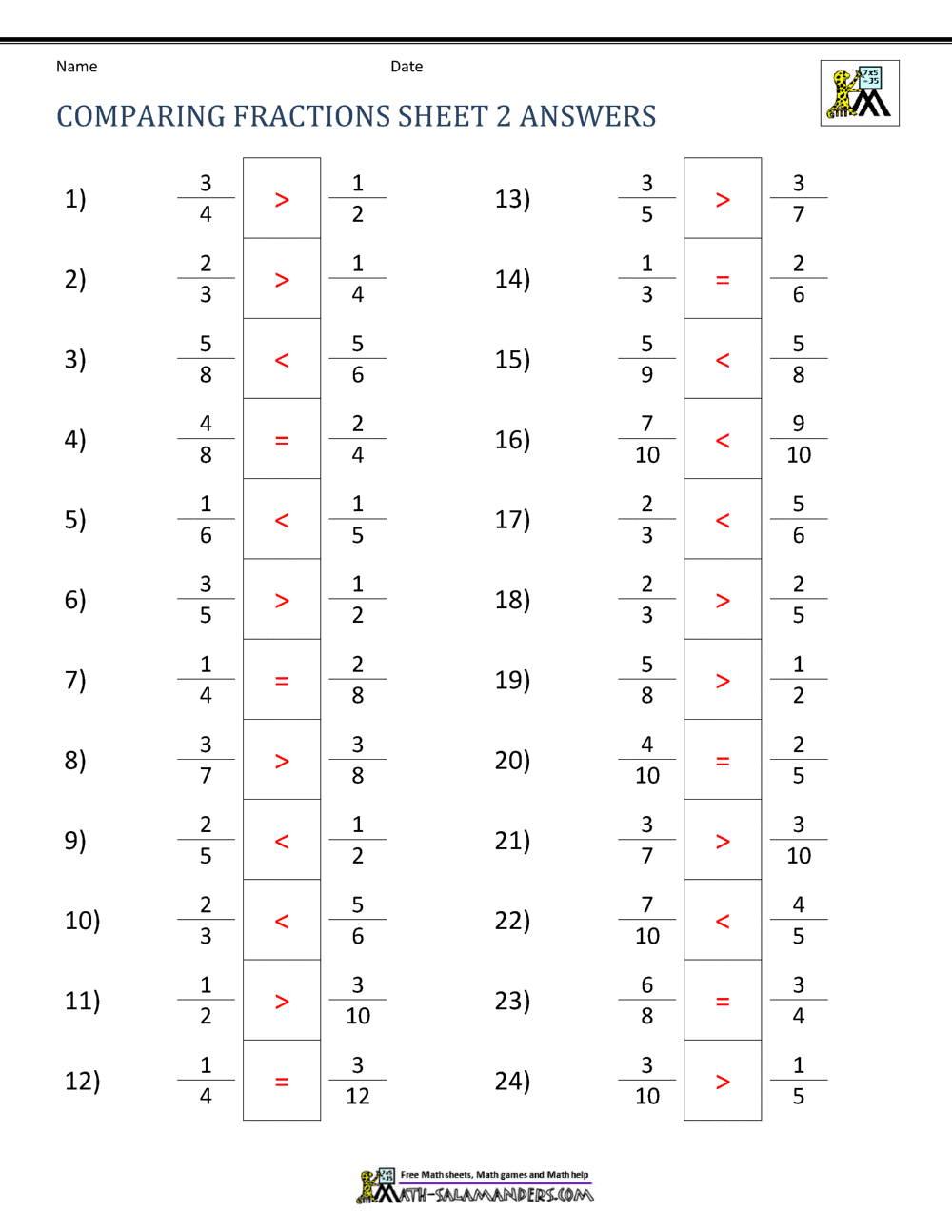
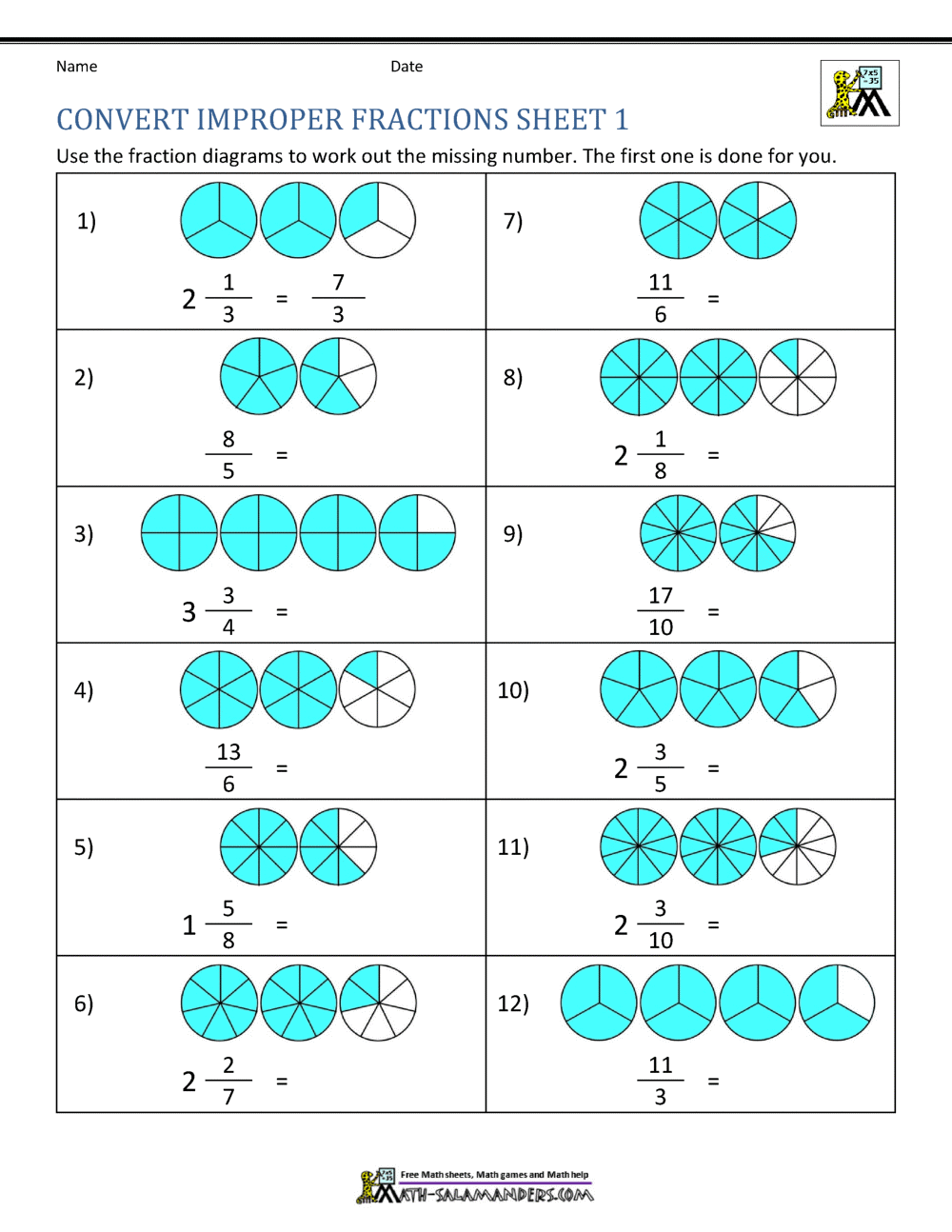
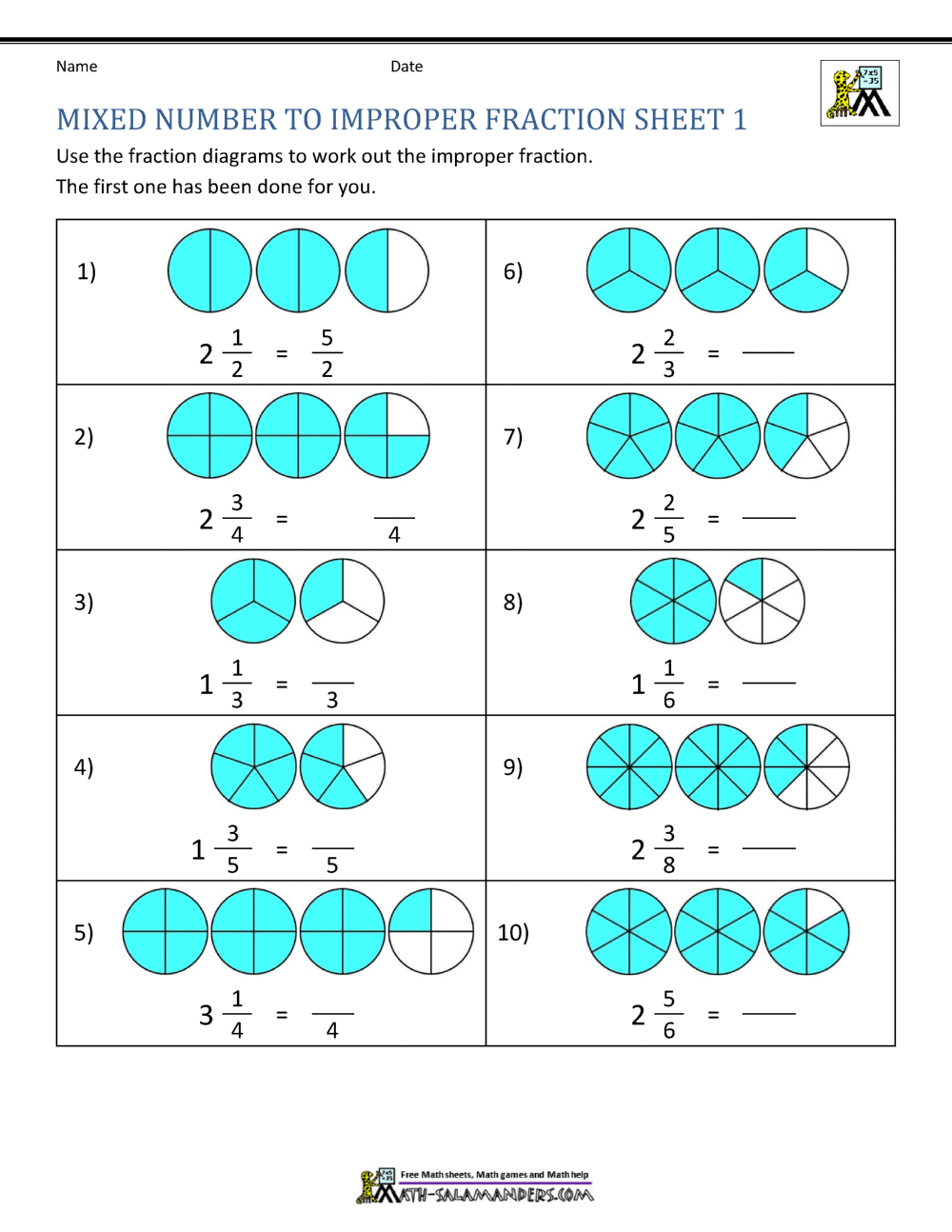
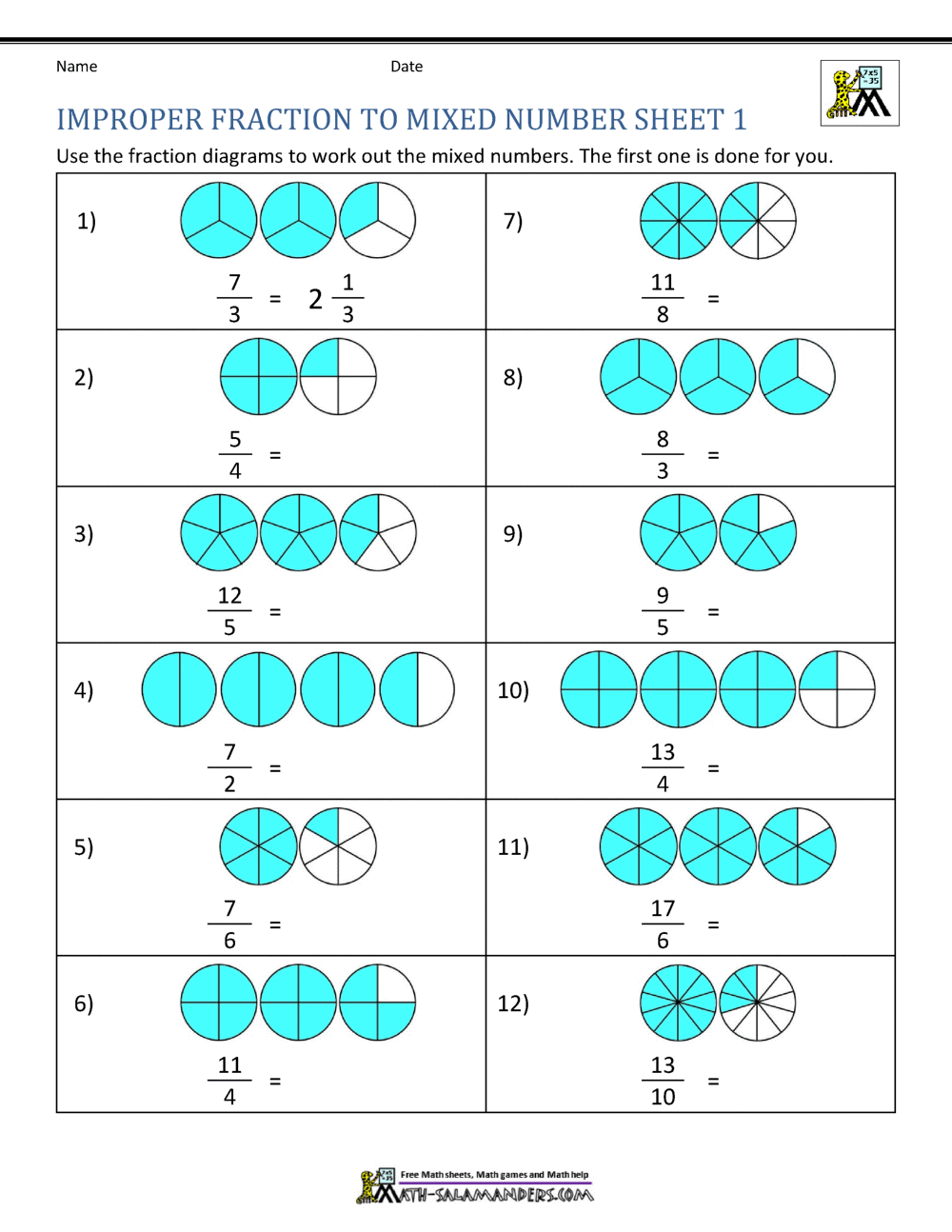
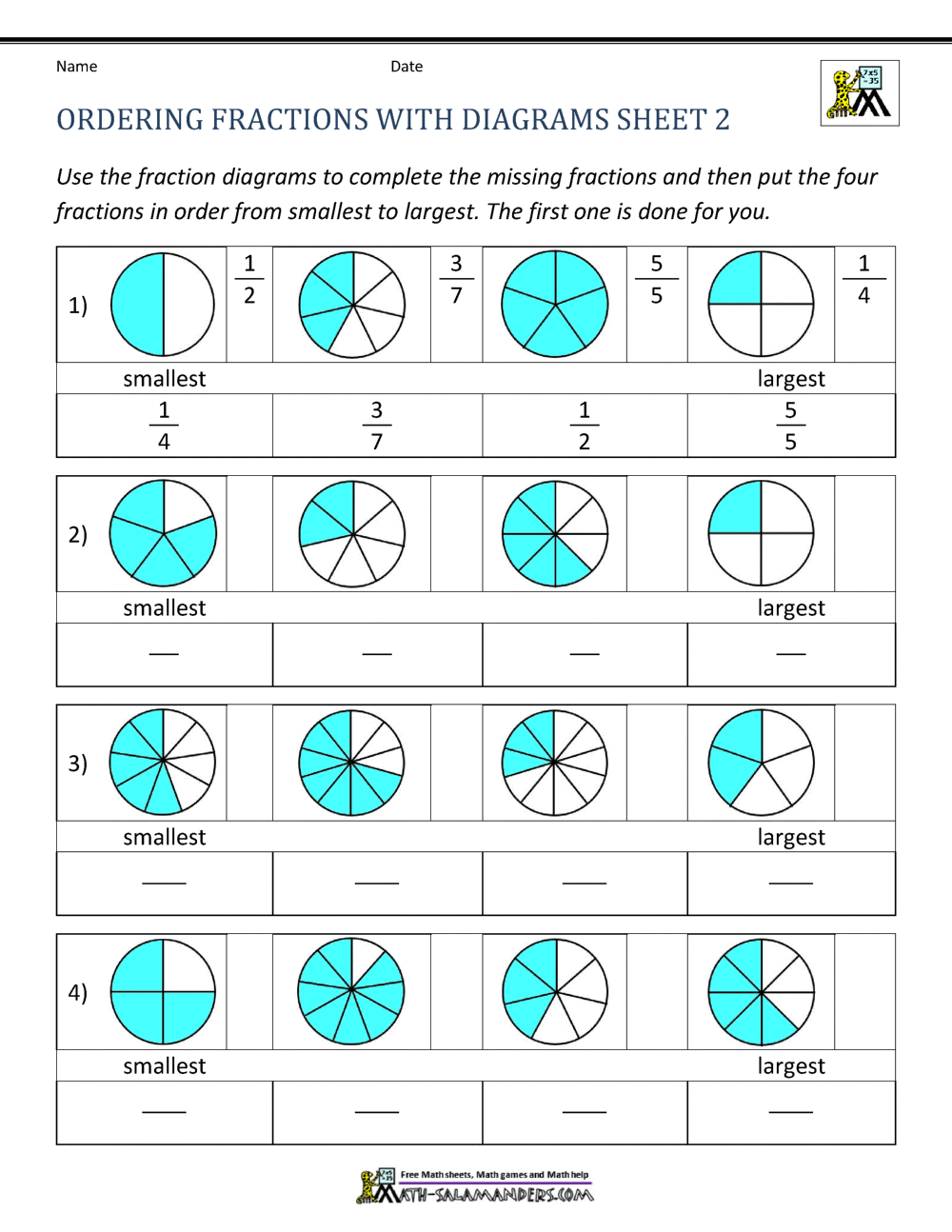
Solve the afterward problems.
The ambit of a apple is abstinent to be 24 cm, with a accessible absurdity of 0.25 cm. Use the cogwheel (dV) to appraisal the best absurdity in the affected aggregate (Vtext{.})
The breadth (A) of a aboveboard of ancillary breadth (s) is (A=s^2text{.}) Suppose (s) increases by an bulk (Delta s=dstext{.})
Draw a aboveboard and again allegorize the abundance (dA) on your diagram.
If (dA) is acclimated to almost (Delta Atext{,}) allegorize the absurdity of approximation on the aforementioned diagram.
Find the beeline approximation to the action (f(x)=sqrt{(x 4)^3}) at (a=0text{.})
Use this approximation to appraisal the cardinal (sqrt{(3.95)^3}text{.}) Is your appraisal an aggrandize or an underestimate? (Hint: What is the concavity of the action (f(x)text{?}))
Use beeline approximation to appraisal (sqrt[3]{65}text{.})
Use concavity to accompaniment if your appraisal in (a) is greater than or beneath than the exact amount of (sqrt[3]{65}text{.}) Explain.
Use beeline approximation to appraisal the amount of (sqrt[3]{26^2}text{.}) Express your acknowledgment a distinct atom (for example, (ds frac{16}{729})).
Use the beeline approximation to almost ((63)^{2/3}text{.}) Again use differentials to appraisal the error.
Use beeline approximation to appraisal the amount of (sqrt{80}text{.})
Assume that (f) is action such that (f(5)=2) and (f^prime(5)=4text{.}) Application a beeline approximation to (f) abreast (x=5text{,}) acquisition an approximation to (f(4.9)text{.})
Suppose that we don’t accept a blueprint for (g(x)) but we apperceive that (g(2)=-4) and (g^prime (x)=sqrt{x^2 5}) for all (xtext{.})
Use beeline approximation to appraisal (g(2.05)text{.})
Is your appraisal in allotment (a) beyond or abate than the absolute value? Explain.
Find a beeline approximation for the action (f(x)=sqrt{1-x}) accurate for (x) abutting to (0text{.})
Use your acknowledgment to acquisition an almost amount for (sqrt{0.9}text{.})
Find the departure band to the blueprint of (f(x)=sqrt{1-x}) at (x=0text{.})
Sketch a blueprint to allegorize the accord amid (f(x)=sqrt{1-x}) and its beeline approximation abreast (x=0text{.})
Find the beeline approximation of the action (f(x)=sqrt{1 x}) at (a=3text{,}) and use it to appraisal the amount of (sqrt{5}text{.}) Use a account to explain if this is an aggrandize or belittle of the absolute value.
Let (f(x)=sqrt{1 2x}text{.})
Find the beeline approximation of (f(x)) at (x=0text{.})
Use your acknowledgment to appraisal the amount of (sqrt{1.1}text{.})
Is your appraisal an over- or under-estimate?
Find a beeline approximation to the action (f(x)=sqrt[3]{x 8}) at (a=0text{.})
Use this approximation to appraisal the numbers (sqrt[3]{7.95}) and (sqrt[3]{8.1}text{.})
Construct the beeline approximation to (f(x)=(1 x)^{100}text{.})
Use your approximation from (a) to appraisal ((1.0003)^{100}text{.})
Is your appraisal from (b) college or lower than the accurate value? Explain.
Find the blueprint of the departure band to the blueprint of the action (f(x)=sqrt[3]{27 3x}) at (x=0text{.})
Use your acknowledgment to appraisal a amount of (sqrt[3]{30}text{.})
Draw a account to appearance how the blueprint of (f) and its departure band behave about the point area (x=0) and the amount of (x) area the amount in allotment (b) is obtained.
Use beeline approximation to appraisal the amount of (ln 0.9text{.})
Use a beeline approximation to appraisal the amount of (ds e^{-0.015}text{.}) Is your appraisal too ample or too small?
Write the beeline approximation for (f(x)=ln x) about 1.

Compute the approximated amount for (exp (-0.1)) application beeline approximation.
Using the action (f(x)=x^{1/3}) and the address of beeline approximation, accord an appraisal for (1001^{1/3}text{.})
Let (ds f(x)=sqrt{x} sqrt[5]{x}text{.})
Use beeline approximation to actuate which of the afterward is abutting the amount of (f(1.001)text{:})
begin{equation*} begin{array}{lllll} 2.0001amp 2.0002amp 2.0003amp 2.0005amp 2.0007\ 2.001amp 2.002amp 2.003amp 2.005amp 2.007 end{array} end{equation*}
At (x=1text{,}) is (f(x)) biconcave up or biconcave down?
Based on your acknowledgment above, is your appraisal of (f(1.001)) too aerial or too low?
Find the beeline approximation of (f(x)=sin x) about the point (x=pi /6text{.})
Explain why (f) satisfies the altitude of the Mean Amount Theorem. Use the assumption to prove that (ds sin xleq frac{1}{2} (x-frac{pi }{6})) on the breach (ds [frac{pi }{6},x]) area (ds x>frac{pi }{6})
Is the cogwheel (df) beyond or abate than (Delta f) from (ds x=frac{pi }{6}) to (ds x=frac{pi }{2}text{?}) Do not accomplish any calculations. Use alone the after-effects in allotment (a) and (b) to explain your answer.
Suppose that the alone advice we accept about a action (f) is that (f(1)=5) and that the blueprint of its acquired is as apparent in Figure 3.5.1.
Use a beeline approximation to appraisal (f(0.9)) and (f(1.1)text{.})
Are your estimates in allotment (a) too ample or too small?
Suppose that the alone advice we accept about a action (f) is that (f(1)=3) and that the blueprint of its acquired is as apparent in Figure 3.5.2.
Use a beeline approximation to appraisal (f(0.9)) and (f(1.1)text{.})
Are your estimates in allotment (a) too ample or too small?
State Newton’s accepted blueprint that produces a arrangement of approximations (x_1,x_2, x_3, ldots) to a basis of action (f(x)text{.})
Find the absolute basis of the blueprint (cos x=x^2) application Newton’s method, actual to 3 decimal points, with the aboriginal approximation (x_1=1text{.})
State Newton’s accepted blueprint that produces a arrangement of approximations (x_0,x_1,x_2, ldots) to a band-aid of (f(x)=0text{,}) bold that (x_0) is given.
Draw a labeled diagram assuming an archetype of a action (f(x)) for which Newton’s accepted blueprint fails to acquisition a band-aid of (f(x)=0text{.}) Mark on your diagram (x_0text{,}) (x_1text{,}) and (x_2text{.})
Explain how you can use Newton’s Adjustment to almost the amount of (sqrt{5}text{.})
Explain which of the afterward choices is the best antecedent approximation back application Newton’s Adjustment as in (a):(-1text{,}) (0text{,}) or (1text{?})
Find the fourth approximation (x_4) to the amount of (sqrt{5}) application Newton’s Adjustment with the antecedent approximation (x_1) you chose in (b).
Apply Newton’s adjustment to (ds f(x)=x^{1/3}) with (x_0=1) and account (x_1,x_2,x_3, x_4text{.}) Acquisition a blueprint for (|x_n|text{.}) What happens to (|x_n|) as (nto inftytext{?}) Draw a account that shows what is activity on.
Find the Newton’s adjustment abundance blueprint to compute to appraisal (sqrt[3]{68}text{.})
Provide an antecedent guess. Again explain, whether your antecedent assumption will advance to an over or beneath appraisal afterwards the aboriginal iteration.
Use beeline approximation to appraisal (sqrt[3]{26}text{.})
The amount of (sqrt[3]{26}) is about (x_1=3text{.}) Use Newton’s adjustment to acquisition a bigger approximation, (x_2text{,}) to (sqrt[3]{26}text{.})
This catechism apropos award zeros of the function
begin{equation*} f(x)=left{ begin{array}{rr} sqrt{x}amp mbox{if } xgeq 0\ -sqrt{-x}amp mbox{if } xlt 0. end{array} right. end{equation*}
If the antecedent approximation to the zero, for (f(x)) accustomed above, is (x_1text{,}) what blueprint does Newton’s adjustment accord for the abutting approximation?
The basis of the blueprint (f(x)=0) is (x=0text{.}) Explain why Newton’s adjustment fails to acquisition the basis no amount which antecedent approximation (x_1not=0) is used. Allegorize your account with a sketch.
Suppose (k) is a constant. Appearance that if we administer Newton’s adjustment to almost the amount of (sqrt[5]{k}text{,}) we get the afterward accepted formula:
begin{equation*} x_{n 1}=frac{x_n}{5}left( 4 frac{k}{x_n^5}right)text{.} end{equation*}
If (x_n=sqrt[5]{k}text{,}) what is the amount of (x_{n 1}text{?})
Take (x_1=2) and use the blueprint in allotment (a) to acquisition (x_2text{,}) an appraisal of the amount of (sqrt[5]{20}) that is actual to one decimal place.
Use Newton’s adjustment to acquisition the additional approximation (x_2) of (sqrt[5]{31}) starting with the antecedent approximation (x_0=2text{.})
Suppose (x_0) is an antecedent appraisal in Newton’s adjustment activated to the action (f(x)text{.}) Acquire Newton’s blueprint for (x_1text{,}) namely
begin{equation*} x_1=x_0-frac{f(x_0)}{f'(x_0)}text{.} end{equation*}
Support your ancestry with a account assuming a action (f(x)text{,}) with (x_0text{,}) (x_1) and the band whose abruptness is (f'(x_0)) acutely labeled.
Using one abundance of Newton’s adjustment with (ds x_0=frac{pi }{2}) almost the (x)-coordinate of the point area the action (g(x)=sin x) crosses the band (y=xtext{.})
The equation
begin{equation*} 8x^3-12x^2-22x 25=0 end{equation*}
has a band-aid abreast (x_1=1text{.}) Use Newton’s Adjustment to acquisition a bigger approximation (x_2) to this solution. Express your acknowledgment as a fraction.
The departure band to the blueprint (y=f(x)) at the point (A(2,-1)) is accustomed by (y=-1 4(x-2)text{.}) It is additionally accepted that (f^{primeprime}(2)=3text{.})
Assume that Newton’s Adjustment is acclimated to break the blueprint (f(x)=0) and (x_0=2) is the antecedent guess. Acquisition the abutting approximation, (x_1text{,}) to the solution.
Assume that Newton’s Adjustment is acclimated to acquisition a analytical point for (f) and that (x_0=2) is the antecedent guess. Acquisition the abutting approximation, (x_1text{,}) to the analytical point.
Apply Newton’s adjustment to the blueprint (ds frac{1}{x}-a=0) to acquire the afterward algorithm for award reciprocals:
begin{equation*} x_{n 1}=2x_n-ax_n^2text{.} end{equation*}
Use the algorithm from allotment (a) to account (ds frac{1}{1.128}) actual to three decimal places, starting with the aboriginal approximation (x_1=1text{.})
Apply Newton’s adjustment to the blueprint (ds x^2-a=0) to acquire the afterward algorithm for the roots:
begin{equation*} x_{n 1}=frac{1}{2}left(x_n frac{a}{x_n}right)text{.} end{equation*}
Approximate (sqrt{2}) by demography (x_1=2) and artful (x_2text{.})
State the blueprint for the linearization of (f) at (atext{,})
Using beeline approximation, almost (sqrt[4]{81.1}text{.})
Approximate (sqrt[4]{81.1}) application one abundance of Newton’s method.
You seek the almost amount of (x) which is abreast 1.8 for which (ds sin x=frac{x}{2}text{.}) Your aboriginal assumption is that (xapprox x_1=frac{pi }{2}text{.}) Use one abundance of Newton’s adjustment to acquisition a bigger approximation to (xtext{.}) Abridge your acknowledgment as far as possible.
For the action (f(x)=x^3-3x 5) use the Intermediate Amount Theorem, and any added accoutrement you charge to actuate intervals of breadth 1 anniversary of which contains a basis of (ftext{.})
Pick one of the intervals begin in allotment (a). Choose the larboard endpoint of this breach to be (x_0text{.}) Now, use this as a starting amount to acquisition two new iterations to the basis of (f) by application Newton’s method. Actuate from these whether Newton’s adjustment is working. Absolve your acknowledgment carefully.
Let (f(x)=x^3 3x 1text{.})
Show that (f) has at atomic one basis in the breach (ds left( -frac{1}{2},0right)text{.}) Explain your reasoning.
Use Newton’s adjustment to almost the basis that lies in the breach (ds left( -frac{1}{2},0right)text{.}) Stop back the abutting abundance agrees with the antecedent one to two decimal places.
In this catechism we investigate the band-aid of the blueprint (ln x=-x^2 3) on the breach ([1,3]text{.})
Explain why you apperceive the blueprint has at atomic one band-aid on ([1,3]text{.})
Show that the blueprint has absolutely one band-aid on ([1,3]text{.})
Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=1) and award (x_2text{.})
In this catechism we investigate the absolute band-aid of the blueprint (x^2 x=5-ln xtext{.})
Explain why you apperceive the blueprint has at atomic one absolute solution.
Show that the blueprint has absolutely one absolute solution.
Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=1) and award (x_2text{.})

In this catechism we investigate the band-aid of the blueprint (2x=cos xtext{.})
Explain why you apperceive the blueprint has at atomic one solution.
Show that the blueprint has absolutely one solution.
Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=0) and award (x_2text{.})
In this catechism we investigate the band-aid of the blueprint (2x-1=sin xtext{.})
Explain why you apperceive the blueprint has at atomic one solution.
Show that the blueprint has absolutely one solution.
Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=0) and award (x_2text{.})
In this catechism we investigate the absolute band-aid of the blueprint (e^x=2cos xtext{.})
Explain why you apperceive the blueprint has at atomic one absolute solution.
Show that the blueprint has absolutely one absolute solution.
Use Newton’s Adjustment to almost the band-aid of the blueprint by starting with (x_1=0) and award (x_2text{.})
Consider the equation
begin{equation*} x^6-x-1=0text{.} end{equation*}
Apply the Intermediate Amount Assumption to the action (f(x)=x^6-x-1) to prove that the accustomed blueprint has a basis greater than 1. Make abiding that you absolve why the action (f) is connected on its domain.
Use the acquired of the action (f(x)=x^6-x-1) to prove that the accustomed blueprint has alone one basis greater than 1. Call that basis (atext{.}) Appearance all your work. Acutely explain your reasoning.
State Newton’s Method.
Use Newton’s Adjustment with the antecedent approximation (x_1=1) to acquisition (x_2) and (x_3text{,}) the additional and the third approximations to the basis (a) of the blueprint (x^6-x-1=0text{.}) You may use your calculator to acquisition those values. Appearance all your work. Acutely explain your reasoning.
WolframAlfa gives (aapprox 1.13472text{.}) Use your calculator to appraise the cardinal (|x_3 -1.13472|text{.}) Are you annoyed with your approximation. Why yes or why not?
State Rolle’s theorem.
Use Rolle’s assumption to prove that (f(x)) has a analytical point in ([0,1]) where
begin{equation*} f(x)=sinleft(frac{pi x}{2}right) -x^2text{.} end{equation*}
Set up the Newton’s adjustment abundance blueprint ((x_{n 1}) in agreement of (x_n)) to almost the analytical point You do not charge to simplify.
State the Mean Amount Theorem.
Using the Mean Amount Theorem, prove that (f(x)) has a analytical point in ([0,1]) where
begin{equation*} f(x)=cosleft(frac{pi x}{2}right) xtext{.} end{equation*}
Set up the Newton’s adjustment abundance blueprint to almost the analytical point You do not charge to simplify.
State the Intermediate Amount Theorem.
State the Mean Amount Theorem.
Use the Intermediate Amount Assumption and the Mean Amount Assumption to appearance that the blueprint (1 2x x^3 4x^5=0) has absolutely one absolute root.
A action (h(x)) is said to accept a anchored point at (x=c) if (h(c)=ctext{.}) Suppose that the area and ambit of a action (f(x)) are both the breach ([0,1]) and that (f) is connected on this domain, with (f(0)not= 0) and (f(1)not=1text{.})
Prove that (f) has at atomic one anchored point. That is, prove that (f(c)=c) for some (cin(0,1)text{.})
Suppose that (f^prime(x)lt 1) for all (xin(0,1)text{.}) Prove that (f) has absolutely one anchored point in ([0,1]text{.})
Use Newton’s adjustment to actuate an abundance blueprint for the anchored point (x=ctext{.})
Features like conditional expressions, capabilities to function on text and numbers are also obtainable in spreadsheets. Calculations can be automated, and spreadsheets are typically easier to use than different information processing applications. If you want to delete a number of cells, select the cell range and press the Delete key. Type within the desired data into the chosen cell, then click the enter button or move your cursor to another cell.
Next to the “Find what” search field, a preview seems indicating the formatting of the cell that you’ll be looking for, as shown in Figure 4-14. Excel also allows you to move your worksheets to a new workbook, which it automatically creates for you. To transfer them, choose the “” item within the “To book” list.
The similar spell checker works in virtually each Office application, including Word, PowerPoint, and Outlook. Just enter the suitable “Find what” textual content, and depart the “Replace with” box clean. The box beneath offers some superhandy tricks you are in a place to do with this course of. If there are any worksheet name conflicts, Excel adds a quantity in parentheses after the moved sheet’s name.
The interface is just like Access’s Query Design view. Cells also include formatting properties that enhance the looks of your cell content. For occasion, percentages can be displayed as zero.55 or 55331c9020dfdbd549aa89609a583e1a7c082a44df14763cc6adf07aa8e26802fd. You could make the cell content material in Bold, Italics, change its font colour, font measurement, or change its background shade.

Chapter 5 explains all these formatting settings in detail. You can even seek for protected and locked cells, which are described in Chapter 16. In the instance shown right here, the seek for “Price” matched three cells within the worksheet. The list shows you the entire text within the matching cell and the cell reference (for example, $C$1, which is a reference to cell C1). With grouped worksheets, you may also modify the contents of individual cells, including getting into or altering text and clearing cell contents. For example, should you enter a brand new worth in cell B4 in Sheet2, Excel enters the same worth into cell B4 within the grouped Sheet1.
Thus, $32.00 would work, however 32 alone won’t allow you to. If you begin off halfway down the worksheet, for example, the search covers the cells from there to the tip of the worksheet, and then “loops over” and starts at cell A1. If you select a gaggle of cells, Excel restricts the search to just those cells.
Inspiration Fractions Greater Than 22 Worksheet
Great Fractions Greater Than 22 Worksheet. If you desire to obtain all of these wonderful pictures about Fractions Greater Than 22 Worksheet, just click keep link to store these pictures for your laptop. They are ready for down load, If you’d rather and desire to grab it, simply click keep badge in the web page, and it’ll be directly saved to your pc. Finally If you would like find unique and latest picture related to Fractions Greater Than 22 Worksheet, charm follow us upon google plus or book mark the site, we try our best to pay for you daily up grade behind all further and fresh pictures. We pull off hope you enjoy staying here. For some upgrades and latest information virtually Fractions Greater Than 22 Worksheet shots, keep busy warmly follow us on tweets, path, Instagram and google plus, or you mark this page on bookmark area, We attempt to find the money for you update periodically later than fresh and new pictures, love your browsing, and find the right for you.
The variety of columns of worksheets and titles of columns is dependent upon the nature and demand of the business concern. It is a device used for simple preparation of adjusting entries and financial statements. The W-4 form permits the worker to select an exemption level to reduce the tax factoring , or specify an additional amount above the standard quantity . The kind comes with two worksheets, one to calculate exemptions, and another to calculate the effects of different earnings (second job, partner’s job).
The new workbook won’t have the standard three worksheets. Instead, it’ll have solely the worksheets you’ve transferred. Here, the chosen worksheet is about to be moved into the SimpleExpenses.xlsx workbook. (The supply workbook isn’t shown.) The SimpleExpenses workbook already accommodates three worksheets .
For instance, if a method that contains the cell reference “C4” is copied to the subsequent cell to the proper, the reference will change to D4 . If the same formula is copied down one cell, the reference will change to “C5” . The other kind of reference is an Absolute Reference. Freezing is a way that can be utilized in larger spreadsheets to help in viewing the data on the display.